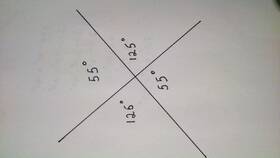
Вертикальные углы - это пары углов, образованные при пересечении двух прямых. Они обладают важным геометрическим свойством, которое часто используется при решении задач.
Содержание
Вертикальные углы - это пары углов, образованные при пересечении двух прямых. Они обладают важным геометрическим свойством, которое часто используется при решении задач.
Основное свойство вертикальных углов
Ключевая особенность вертикальных углов заключается в следующем:
- Вертикальные углы всегда равны между собой
- Сумма всех четырех углов, образованных пересекающимися прямыми, равна 360°
Геометрическая иллюстрация
| Углы | Свойство |
| ∠1 и ∠3 | Вертикальные (равны) |
| ∠2 и ∠4 | Вертикальные (равны) |
| ∠1 + ∠2 + ∠3 + ∠4 | 360° |
Почему вертикальные углы равны
Равенство вертикальных углов можно доказать следующим образом:
- При пересечении прямых образуются смежные углы
- Сумма смежных углов всегда равна 180°
- Если ∠1 + ∠2 = 180° и ∠2 + ∠3 = 180°
- Тогда ∠1 = ∠3 (вертикальные углы равны)
Практическое применение
Свойства вертикальных углов используются:
- В архитектуре при проектировании конструкций
- В геодезии при проведении измерений
- В навигации для определения направлений
- В решении геометрических задач
Пример расчета
| Если один вертикальный угол равен 45° | Тогда противоположный ему угол тоже равен 45° |
| Сумма двух вертикальных углов | 45° + 45° = 90° |
| Сумма всех четырех углов | 45° + 135° + 45° + 135° = 360° |
Важные выводы
- Вертикальные углы всегда равны между собой
- Сумма двух вертикальных углов может быть разной (но сами углы равны)
- Полная сумма всех четырех углов при пересечении прямых равна 360°
- Это свойство не зависит от вида пересекающихся прямых
Знание свойств вертикальных углов помогает решать множество геометрических задач и понимать основы построения различных фигур.
